miércoles, 16 de marzo de 2016

POLÍGONOS REGULARES


POLÍGONOS REGULARES

En geometría, se denomina polígono regular a un polígono cuyos lados y ángulos interiores son congruentes entre sí. Los polígonos regulares de tres y cuatro lados se llaman triángulo equilátero y cuadrado, respectivamente. Para polígonos de más lados, se añade el término regular (pentágono regular, hexágono regular, octágono regular, etc). Solo algunos polígonos regulares pueden ser construidos con regla y compás.

Existen diversas fórmulas para calcular el área de un polígono regular, dependiendo de los elementos conocidos.

En función del perímetro y la apotema[editar]

El área de un polígono regular, conociendo el perímetro y la apotema es:
A = \frac {P \cdot a}{2}
[Expandir]Demostración

En función del número de lados y la apotema[editar]

PoliReg 04.svg
Sabiendo que:
A_p = \frac {L \cdot n \cdot a} {2}
Además  \delta = \frac {\pi} {n} \ , ya que es la mitad de un ángulo central (esto en radianes).
Observando la imagen, es posible deducir que:
L = 2 \cdot a \cdot \tan \left ( \frac {\pi} {n} \right )
Sustituyendo el lado:
A_p = \frac { \left ( 2 \cdot a \cdot \tan \left ( \frac {\pi} {n} \right ) \right ) \cdot n \cdot a } {2}
Finalmente:
A_p = a^2 \cdot n \cdot \tan \left ( \frac {\pi} {n} \right )
Con esta fórmula se puede averiguar el área con el número de lados y la apotema, sin necesidad de recurrir al perímetro.

En función del número de lados y el radio[editar]

Un polígono queda perfectamente definido por su número de lados n, y el radio r, por tanto podemos determinar cual es su área, a la vista de la figura, tenemos que:
L = 2 r \sin({\delta}) \;
a = r \cos({\delta}) \;
donde el ángulo central es:
\alpha = 2 \delta = \frac{2\pi}{n} \;
sabiendo que el área de un polígono es:
A_p = \frac{L \cdot n \cdot a}{2} \;
y sustituyendo el valor del lado y la apotema calculados antes, tenemos:
A_p = \frac{2 r \sin({\delta}) \cdot n \cdot r \cos({\delta})}{2} \;
ordenando tenemos:
A_p = \frac{n r^2 \cdot 2 \sin({\delta}) \cos({\delta})}{2} \;
sabiendo que:
2 \sin({\delta}) \cos({\delta}) = \sin({2 \delta}) \;
resulta:
A_p = \frac{n r^2 \sin({\alpha})}{2} \;
o lo que es lo mismo:
A_p = \frac{n r^2 \sin({\frac{2\pi}{n}})}{2} \;
Con esta expresión podemos calcular el área del polígono, conociendo solamente el número de lados y su radio, lo que resulta útil en muchos casos.
Publicado por en

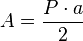
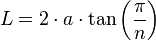
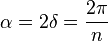
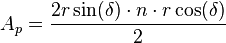
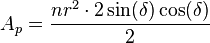
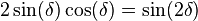
No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)