GRAFICAR FRACCIONES HETEROGÉNEAS
Representación gráfica y analítica[editar]
Suele utilizarse la figura geométrica (que representa la unidad) seccionada en una cantidad de partes iguales para mostrar el denominador, y se colorean (u omiten) las que se toman para distinguir la cantidad que indica el numerador.
- Notación y convenciones:
- En una fracción común, el denominador se lee como número partitivo (ejemplos: 1/4 se lee «un cuarto», 3/5 se lee «tres quintos»);
- Una fracción negativa se escribe con el signo menos delante de la fracción (ejemplos: -1/4 o
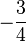 , pero no 3/-4);
, pero no 3/-4); - Una fracción genérica a/b representa el producto de a por el recíproco (multiplicativo) de b, de tal modo que
 ; si tanto a como b son números negativos
; si tanto a como b son números negativos 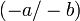 , el producto es positivo, por lo que se escribe: a/b;
, el producto es positivo, por lo que se escribe: a/b; - Toda expresión matemática escrita en esta forma recibe el nombre de «fracción».
La expresión genérica  representa una división algebraica, por lo que el divisor debe ser distinto de cero (b
representa una división algebraica, por lo que el divisor debe ser distinto de cero (b 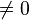 ); el cociente de esta división admite un desarrollo decimal (un número decimal, en el sistema de numeración decimal tradicional) que puede ser finito o infinito periódico (ver Número periódico).
); el cociente de esta división admite un desarrollo decimal (un número decimal, en el sistema de numeración decimal tradicional) que puede ser finito o infinito periódico (ver Número periódico).
 representa una división algebraica, por lo que el divisor debe ser distinto de cero (b
representa una división algebraica, por lo que el divisor debe ser distinto de cero (b 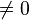 ); el cociente de esta división admite un desarrollo decimal (un número decimal, en el sistema de numeración decimal tradicional) que puede ser finito o infinito periódico (ver Número periódico).
); el cociente de esta división admite un desarrollo decimal (un número decimal, en el sistema de numeración decimal tradicional) que puede ser finito o infinito periódico (ver Número periódico).
Un número irracional no admite una escritura en forma de número fraccionario, o de razón, su expansión decimal será infinita no-periódica, como por ejemplo el número π, el número e, el número áureo y algunas raíces cuadradas y cúbicas.
Tipos de fracciones[editar]
Fracción simple, común o vulgar[editar]
Una fracción simple (también conocida como fracción común o fracción vulgar es un número racional de la forma a/b, donde a y b son números enteros y b≠0. Puesto que una fracción común representa un número racional, las fracciones comunes heredan todas las propiedades matemáticas de los racionales. Ejemplo 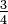 ; 3/4; 3/4; (¾); fracción tres cuartos: numerador 3 y denominador 4, representa al número decimal 0.75, en porcentaje: 75%.
; 3/4; 3/4; (¾); fracción tres cuartos: numerador 3 y denominador 4, representa al número decimal 0.75, en porcentaje: 75%.
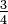 ; 3/4; 3/4; (¾); fracción tres cuartos: numerador 3 y denominador 4, representa al número decimal 0.75, en porcentaje: 75%.
; 3/4; 3/4; (¾); fracción tres cuartos: numerador 3 y denominador 4, representa al número decimal 0.75, en porcentaje: 75%.Fracción propia e impropia[editar]
Las fracciones comunes pueden clasificarse en propias e impropias. Una fracción propia es aquella en la que, si numerador y denominador son positivos, el numerador es menor que el denominador, por ejemplo 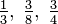 . Por el contrario, una fracción impropia será la fracción en donde el numerador es mayor que el denominador, por ejemplo
. Por el contrario, una fracción impropia será la fracción en donde el numerador es mayor que el denominador, por ejemplo  . En general, una fracción común es una fracción propia si el valor absoluto es estrictamente menor que uno — es decir, si la fracción es mayor que −1 y menor que 1 —.2 3
. En general, una fracción común es una fracción propia si el valor absoluto es estrictamente menor que uno — es decir, si la fracción es mayor que −1 y menor que 1 —.2 3
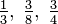 . Por el contrario, una fracción impropia será la fracción en donde el numerador es mayor que el denominador, por ejemplo
. Por el contrario, una fracción impropia será la fracción en donde el numerador es mayor que el denominador, por ejemplo  . En general, una fracción común es una fracción propia si el valor absoluto es estrictamente menor que uno — es decir, si la fracción es mayor que −1 y menor que 1 —.2 3
. En general, una fracción común es una fracción propia si el valor absoluto es estrictamente menor que uno — es decir, si la fracción es mayor que −1 y menor que 1 —.2 3Número mixto[editar]
Un número mixto es la representación de una fracción impropia, en forma de número entero y fracción propia; es una manera práctica de escribir unidades de medida (peso, tiempo, capacidad), recetas de cocina, etc.4
Toda fracción impropia 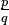 puede escribirse como número mixto:
puede escribirse como número mixto: 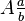 , en donde
, en donde 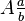 denota
denota 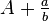 (donde
(donde 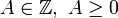 , es la parte entera). Como ejemplos:
, es la parte entera). Como ejemplos:
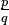 puede escribirse como número mixto:
puede escribirse como número mixto: 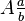 , en donde
, en donde 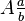 denota
denota 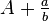 (donde
(donde 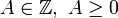 , es la parte entera). Como ejemplos:
, es la parte entera). Como ejemplos: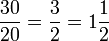 «Una cucharadita y media de...»
«Una cucharadita y media de...»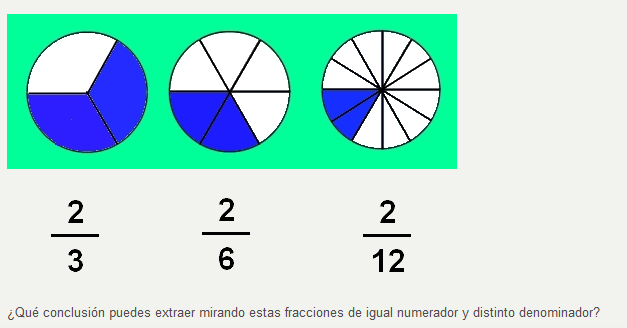


No hay comentarios:
Publicar un comentario