ÁREA DE TRAPECIOS

ÁREA DE TRAPECIOS

Trapecio (geometría)

En geometría, se llama trapecio a un cuadrilátero que tiene dos lados no consecutivos paralelos llamados bases del trapecio y la distancia entre ellos altura.¹ Se denominamediana al segmento que tiene por extremos los puntos medios de los lados no paralelos. Esta definición de trapecio determina tres clases de cuadriláteros convexos:trapezoides, ningún par de lados paralelos; trapecios, un solo par de lados paralelos; paralelogramos, dos pares de lados paralelos. ²

Los trapecios respecto a sus ángulos internos, pueden ser rectángulos, isósceles o escalenos:

Trapecio rectángulo

Trapecio isósceles

Trapecio escaleno

• Trapecio rectángulo es el que tiene un lado perpendicular a sus bases.

Tiene dos ángulos internos rectos, uno agudo y otro obtuso.

• Trapecio isósceles es el que tiene los lados no paralelos de igual medida.

Tiene dos ángulos internos agudos y dos obtusos, que son iguales entre sí.

Las diagonales son congruentes.

la suma de los ángulos opuestos es 180°.

El teorema de Euler, en el caso de un trapecio isósceles, se reduce a

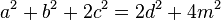
, siendo a y b las bases, c el lado igual y d la diagonal y m el segmento que une los puntos medios de las diagonales.

• Trapecio escaleno es el que no es isósceles ni rectángulo, la medida de sus lados da como resultado medidas diferentes.

Sus cuatro ángulos internos poseen diferentes medidas.

• El segmento que une los puntos medios de sus diagonales es paralela a las bases del trapecio y mide la diferencia de las bases.
• Un trapecio, no rectángulo, puede descomponerse en dos triángulos rectángulos y un rectángulo mediante alturas trazadas de los extremos de la base menor a la base mayor. ³
• Si los lados de un trapecio son respectivamente iguales a los de otro trapecio, los trapecios son iguales.
• Para que un trapecio sea isósceles es necesario y suficiente que los ángulos en la base sean iguales o alternativamente las diagonales sean iguales.
• Las bisectrices de los ángulos adyacentes de un lado lateral forman un ángulo recto y se intersecan en un punto situado en la mediana del trapecio.⁴
• Sobre un paralelogramo, a partir de dos vértices opuestos, sobre los lados paralelos tome sendos puntos equidistanes, luego cuando se los une mediante un segmento, se determinan dos trapecios complementarios e iguales. Esto es, todo paralelogramo se puede descomponer en dos trapecios iguales.
• Todo trapecio isósceles se puede descomponer en dos trapecios rectángulos iguales, mediante un segmento que une los puntos medios de las bases.La recta que contiene al segmento es eje de simetría de las figuras resultantes.
• El baricentro de un trapecio es un punto ubicado en el segmento que une los baricentros de los triángulos que determina una diagonal, más cerca al baricentro del triángulo de mayor área.
• Si se unen dos lados de un triángulo mediante un segmento paralelo al tercer lado, se generan un triángulo semejante al original y un trapecio. Estas dos figuras tienen interiores disjuntos y un lado común, justamente, el segmento paralelo.⁵ .
• Sobre el lado, de un rectángulo cuya longitud es a unidades, se marca un punto M, que dista m unidades de un vértice, en el lado paralelo se sitúa un punto N, a una distancia a-m del vértice opuesto al primero. Uniendo los puntos M y N se obtienen dos trapecios rectángulos congruentes, con un lado común: el segmento MN.