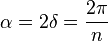LA UNIDAD DE PESO

El Sistema Internacional de Unidades, abreviado SI, es el sistema de unidades que se usa en todos los países del mundo, a excepción de tres que no lo han declarado prioritario o único.

Es el heredero del antiguo Sistema Métrico Decimal y por ello también se conoce como «sistema métrico».

Se instauró en 1960, en la XI Conferencia General de Pesas y Medidas, durante la cual inicialmente se reconocieron seis unidades físicas básicas. En 1971 se añadió la séptima unidad básica: el mol.

Una de las características trascendentales, que constituye la gran ventaja del Sistema Internacional, es que sus unidades se basan en fenómenos físicos fundamentales. Excepción única es la unidad de la magnitud masa, el kilogramo, definida como «la masa del prototipo internacional del kilogramo», un cilindro de platinoe iridio almacenado en una caja fuerte de la Oficina Internacional de Pesas y Medidas.^{nota 1}

Las unidades del SI constituyen referencia internacional de las indicaciones de los instrumentos de medición, a las cuales están referidas mediante una concatenación ininterrumpida de calibraciones o comparaciones.

Esto permite lograr equivalencia de las medidas realizadas con instrumentos similares, utilizados y calibrados en lugares distantes y, por ende, asegurar —sin necesidad de duplicación de ensayos y mediciones— el cumplimiento de las características de los productos que son objeto de transacciones en el comercio internacional, su intercambiabilidad.

Entre los años 2006 y 2009 el SI se unificó con las normas ISO para instaurar el Sistema Internacional de Magnitudes (ISO/IEC 80000, con las siglas ISQ).

Masa (M)

kilogramo (kg)nota 2

Masa del prototipo internacional del kilogramo, adoptado por la Conferencia General de Pesas y Medidas y depositado en la Oficina Internacional de Pesas y Medidas, enSèvres, Francia. Este prototipo es un cilindro de 39 mm de altura y 39 mm de diámetro de una aleación90 % de platino y 10 % de iridio; tiene una densidad de 21 500 kg/m3.

Propuesta de redefinición a un valor relacionado con laconstante de Planck (h).

Elementos del polígono regular

Existen varios elementos del polígono regular que los caracterizan.

• Centro (C): es el punto del polígono regular que equidista a todos los vértices.
• Lado (L): es uno de los n segmentos que delimitan el perímetro del polígono.
• Vértice (V): punto de unión de dos lados. Existen tantos vértices como lados tiene el polígono (n).
• Radio (r): es el segmento que une el centro con un vértice
• Apotema (ap): segmento que une el centro con el punto medio de un lado. Laapotema es perpendicular a dicho lado.

Clasificación de polígonos regulares

Los polígonos regulares se pueden clasificar según el número de lados que tienen:

• Triángulo equilátero: polígono con tres lados y ángulos iguales.
• Cuadrado: polígono con cuatro lados y ángulos iguales.
• Pentágono regular: polígono con cinco lados y ángulos iguales.
• Hexágono regular: polígono con seis lados y ángulos iguales.
• Heptágono regular: polígono con siete lados y ángulos iguales.
• Octógono regular: polígono con ocho lados y ángulos iguales.
• Eneágono regular: polígono con nueve lados y ángulos iguales.
• Decágono regular: polígono con diez lados y ángulos iguales.
• Undecágono regular: polígono con once lados y ángulos iguales.
• Dodecágono regular: polígono con doce lados y ángulos iguales.

Apotema de un polígono regular

La apotema de un polígono regular puede obtenerse sabiendo el número de lados (N) del polígono y lo que mide cada lado (L).

Sea el ángulo central α el ángulo que forman las dos líneas que unen el centro delpolígono (O) y dos vértices consecutivos. Éste se calcula como:


Mediante la tangente de la mitad del ángulo central y un lado (L), se calcula la apotema (ap) del polígono regular.



Área del polígono regular

El área de un polígono regular se calcula a partir de su perímetro y su apotema. Sea P el polígono regular con Nlados, su área es:


En un polígono regular, el perímetro se puede determinar por el producto del número de lados por la longitud de uno de los lados, es decir, Perímetro=N·L. O sea:

EL ÁREA Y LOS POLÍGONOS REGULARES

EL ÁREA Y LOS POLÍGONOS REGULARES

Elementos de un polígono regular

• Lado, L: es cada uno de los segmentos que forman el polígono.
• Vértice, V: el punto de unión de dos lados consecutivos.
• Centro, C: el punto central equidistante de todos los vértices.
• Radio, r: el segmento que une el centro del polígono con uno de sus vértices.
• Apotema, a: segmento perpendicular a un lado, hasta el centro del polígono.
• Diagonal, d: segmento que une dos vértices no contiguos.
• Perímetro, P: es la suma de la medida de su contorno.
• Semiperímetro, SP: es la semisuma del perímetro.
• Sagita, S: parte del radio comprendida entre el punto medio del lado y el arco de circunferencia. La suma de la apotema: a más la sagita: S, es igual al radio: r.

Propiedades de un polígono regular

• Los polígonos regulares son polígonos equiláteros, puesto que todos sus lados son de la misma medida.
• Los polígonos regulares son equiangulares, puesto que todos sus ángulos interiores tienen la misma medida.
• Los polígonos regulares se pueden inscribir en una circunferencia.

Área de un polígono regular[editar]

Existen diversas fórmulas para calcular el área de un polígono regular, dependiendo de los elementos conocidos.

En función del perímetro y la apotema[editar]

El área de un polígono regular, conociendo el perímetro y la apotema es:

[Expandir]Demostración

En función del número de lados y la apotema[editar]

Sabiendo que:

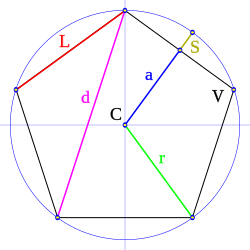
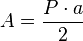
Además , ya que es la mitad de un ángulo central (esto en radianes).

Observando la imagen, es posible deducir que:

Sustituyendo el lado:

Finalmente:

Con esta fórmula se puede averiguar el área con el número de lados y la apotema, sin necesidad de recurrir al perímetro.

En función del número de lados y el radio[editar]

Un polígono queda perfectamente definido por su número de lados n, y el radio r, por tanto podemos determinar cual es su área, a la vista de la figura, tenemos que:

donde el ángulo central es:

sabiendo que el área de un polígono es:

y sustituyendo el valor del lado y la apotema calculados antes, tenemos:

ordenando tenemos:

sabiendo que:

resulta:

o lo que es lo mismo:

Con esta expresión podemos calcular el área del polígono, conociendo solamente el número de lados y su radio, lo que resulta útil en muchos casos.

EL PORCENTAJE

Definición.

Las fracciones con denominador igual a 100 se llaman fracciones porcentajes o, simplemente,  porcentajes. Leemos: 30 por ciento; 28 por ciento; 70 por ciento; y 12 por ciento. Podemos representar gráficamente estos porcentajes igual que se hace con las fracciones. Cálculo de porcentajes ¿Cuánto es el 30% de 200? Para calcular el porcentaje de una cantidad se multiplica la cantidad por el número decimal equivalente al porcentaje 2. Calcula los siguientes porcentajes en tu cuaderno y luego comprueba los resultados en la escena.   Porcentaje Cantidad 10% de 32 25% de 560 32% de 321 5% de 1000 50% de 40 35% de 8 60% de 200 4% de 100 81% de 75 7% de 98   Cambia los valores del porcentaje y de la cantidad. 3. Rellena la siguiente tabla en tu cuaderno utilizando la escena anterior y contesta a las preguntas que siguen: 100% de 100  = 50% de 100 = 25% de 100 = 10% de 100 = 100% de 80  = 50% de 80  = 25% de 80  = 10% de 80  = 100% de 50  = 50% de 50  = 25% de 50  = 10% de 50  = 100% de 20  = 50% de 20  = 25% de 20  = 10% de 20  = 100% de 10  = 50% de 10  = 25% de 10  = 10% de 10  = a) ¿Cuánto es el 100% de una cantidad? b) ¿Por qué número hay que dividir una cantidad para calcular su 50%? ¿Qué fracción es equivalente al 50%? c) ¿Por qué número hay que dividir una cantidad para calcular su 25%? ¿Qué fracción es equivalente al 25%? d) ¿Por qué número hay que dividir una cantidad para calcular su 10%? ¿Qué fracción es equivalente al 10%

EL PERÍMETRO DE LOS POLÍGONOS

EL PERÍMETRO DE LOS POLÍGONOS

1- Polígonos En primer lugar veremos lo relacionado con los polígonos. El perímetro de un polígono es igual a la suma de las longitudes de sus lados y su área es la medida de la región o superficie encerrada por un polígono. 2- Área y perímetro del triángulo - Cálculo del perímetro Es la longitud de su contorno ó la suma de sus lados.   P = a + b + c       Recuerda:   - El perímetro de un triángulo escaleno (todos los lados distinta medida) de lados a, b y c se puede calcular utilizando la siguiente fórmula:   P = a + b + c   - El perímetro de un triángulo isósceles (dos lados igual medida) de lados a y base b se puede calcular utilizando la siguiente fórmula:   P = a + a + b, es decir, P = 2 • a + b   - El perímetro de un triángulo equilátero (todos los lados igual medida)  de lado a se puede calcular utilizando la siguiente fórmula:   P = a + a + a, es decir, P = 3 • a - Cálculo del área Es el producto de uno de sus lados por la altura correspondiente a él, dividido por dos.     3- Área y perímetro del cuadrado   - Cálculo del perímerto Es la longitud de su contorno ó la suma de sus lados   P = a + a + a + a, es decir, P = 4 • a   - Cálculo del área   Para calcular el área de un cadrado multiplicaremos su base por su altura, es decir, su largo por su ancho.   A = lado x lado = lado2   A = a • a A = a2     4- Área y perímetro del rectángulo - Cálculo del perímerto Es la longitud de su contorno ó la suma de sus lados   P = a + a + b + b, es decir, P = 2 • a + 2 • b P = 2 • (a + b)    - Cálculo del área Para calcular el área de un rectángulo multiplicaremos su base por su altura, es decir, su largo por su ancho.     A = base x altura.   A = a • b     5- Área y perímetro del romboide El perímetro del romboide es igual a la suma de las longitudes de sus cuatro lados. P = 2 • a + 2 • b P = 2 • (a + b) - Cálculo del área Se obtiene a partir del área del rectángulo, multiplicando la base por la altura del romboide (no por el otro lado).     A = base x altura     6-  Área y perímetro del rombo   - Cálculo del área Para calcular el área del rombo, recuerda que éste es un cuadrilátero con cuatro lados iguales, paralelos dos a dos.   Si unimos los vértices opuestos, obtenemos su diagonal mayor (la que mide más) y su diagonal menor (la que mide menos) El área del rombo resultará de multiplicar su diagonal mayor por su diagonal menor y dividirlo por dos.     .   - Cálculo del perímerto Sumando las longitudes de los lados de un polígono hallaremos su perímetro.   ¿Cómo calculo  el perímetro si sólo tengo el valor de las diagonales del rombo?     En la figura de arriba, aparece un triángulo coloreado en verde. Ese triángulo está formado por un cateto o lado que es la mitad de la diagonal mayor (D/2), otro cateto o lado que es la mitad de la diagonal menor (d/2) y por la hipotenusa (a), que es a su vez lado del rombo.   Entonces, recordemos, para aplicarlo, el Teorema de Pitágoras:   a2 = b2 + c2   Entonces, si reemplazamos los valores tendremos:     Donde:   D = diagonal mayor d = diagonal menor a = lado   Recuerda ⇒ Los lados de el rombo son iguales. Entonces si por ejemplo el resultado del lado es 6 cm, el perímetro será 6 + 6 + 6 + 6 = 24cm   7- Áreas y perímetros  de polígonos regulares    - Cálculo del perímerto Sumando las longitudes de los lados de un polígono hallaremos su perímetro.   - Cálculo del área Para calcular el área de un polígono regular cualquiera se divide en triángulos uniendo el centro con cada uno de los vértices. La altura de cada uno de los triángulos coincide con la apotema del polígono. Se calcula el área de uno de estos triángulos y se multiplica por el número de triángulos que se han formado.     El área de un polígono regular es igual al producto de su perímetro por su apotema dividido entre dos.   Apotema: segmento que une el centro del polígono con el punto medio de cada lado.   Esta fórmula permite calcular la apotema de cualquier polígono regular.