lunes, 29 de febrero de 2016

SUMA Y RESTA DE FRACCIONES DE DIFERENTE DENOMINADOR

Hay que reducir a común denominador.

1º Se calcula el m.c.m. de los denominadores. Descomponemos en factores

los denominadores y cogemos los factores comunes de mayor exponente y los no comunes.

2º Dividimos el m.c.m. obtenido entre cada uno de los denominadores y

lo que nos dé lo multiplicamos por el número que haya en el numerador.

3º Ya tenemos todas las fracciones con el mismo denominador, sumamos o restamos

los numeradores y dejamos el mismo denominador.

4º Si podemos simplificamos.

Ejemplos

Ejemplos

Ejemplos

FORMA ABREVIADA

SUMA DE FRACCIONES HETEROGENEAS

RESTA DE FRACCIONES HETEROGENEAS

viernes, 26 de febrero de 2016

SUMA Y RESTA DE FRACCIONES HETEROGENEAS

SUMA Y RESTA DE FRACCIONES DE DIFERENTE DENOMINADOR

Hay que reducir a común denominador.

1º Se calcula el m.c.m. de los denominadores. Descomponemos en factores

los denominadores y cogemos los factores comunes de mayor exponente y los no comunes.

2º Dividimos el m.c.m. obtenido entre cada uno de los denominadores y

lo que nos dé lo multiplicamos por el número que haya en el numerador.

3º Ya tenemos todas las fracciones con el mismo denominador, sumamos o restamos

los numeradores y dejamos el mismo denominador.

4º Si podemos simplificamos.

Ejemplos

FORMA ABREVIADA

SUMA DE FRACCIONES HETEROGENEAS

RESTA DE FRACCIONES HETEROGENEAS

miércoles, 24 de febrero de 2016

FRACCIONES HETEROGENEAS

FRACCIONES HOMOGENEAS Y HETEROGENEAS

FRACIONES HOMOGÉNEAS

Se llaman fracciones homogéneas a aquellas que comparten el mismo denominador por ejemplo (3/4 y 5/4) si no comparten el denominador las llamamos fracciones heterogéneas.Si realizamos una suma o adición de fracciones homogéneas, debemos sumar los numeradores y mantener igual el denominador. Veamos un ejemplo de esto:

En caso de realizar sustracciones o restas, procederemos de la misma forma que en una suma, pero en este caso estamos restando. Observemos un ejemplo:

FRACCIONES HETEROGÉNEAS
Se dice que dos fracciones son heterogéneas cuando estas poseen distinto denominador, por lo cual se diferencian de las fracciones homogéneas, que tienen el denominador en común. Si lo que queremos esrealizar sumas o restas con fracciones heterogéneas lo que debemos hacer en primer lugar, es encontrar el común denominador, o sea hallar el mínimo común múltiplo de todos los denominadores. Luego de esto lo que se debe hacer es colocar el denominador común, dividimos entonces el común denominador entre el primer denominador y el resultado lo multiplicamos por el numerador. Repetimos la operación con cada una de las fracciones que tengamos. Por último se suman los resultadosobtenidos y así finalizamos. A veces no es necesario multiplicar entre si los denominadores, eso depende de las fracciones que tengamos. Veamos ahora un ejemplo de suma de fracciones heterogéneas bastante sencillo:

Vemos en el ejemplo anterior que en primer lugar se multiplicaron los denominadores, luego se realizó la multiplicación cruzada. Se sumaron los productospara obtener luego el numerador y finalmente se simplificó la fracción. Observemos otro ejemplo:

jueves, 18 de febrero de 2016

SUMA Y RESTA CON FRACCIONES HOMOGÉNEAS.

Para sumar dos fracciones, hay que tener en cuenta de que existen 2 tipos de fracciones:

1. Fracciones homogéneas (1/4, 2/4, 9/4)
2. Fracciones heterogeneas (1/3, 2/5, 3/7)

Las fracciones homogéneas son las fracciones que tienen el mismo denominador; y las fracciones heterogeneas son las fracciones que tienen diferentes denominadores.

Suma de fracciones homogeneas

Las fracciones homogéneas, en suma, se suman los numeradores y el denominador se queda igual.

Ejemplos:
1/5 + 3/5 = 4/5
2/7 + 9/7 = 11/7

Suma de fracciones heterogéneas

Utilizando un algoritmo sencillo podemos aprender a sumar fracciones mentalmente.

Veamos: Sean a /b y c/d dos fracciones cualesquiera. Si las deseamos sumar podemos seguir la siguiente regla:

a/b + c/d = (ad + bc)/bd
se multiplica cruzado y los productos de suman / se multiplican los denominadores

Ejemplos:
1/4 + 1/3 = (1*3+4*1)/4*3 = (3+4)/12 = 7/12

1/3 + 2/5 = (1*5 + 3*2)/15 = (5+6)/15 = 11/15

1/4 + 1/2 = (2*1 + 4*1)/8 = 6/8
Simplificamos dividiendo por 2 numerador y denominador:
6/8 / 2/2 = 3/4
_______________________________________________________________________

Para restar dos fracciones, hay que tener en cuenta de que existen 2 tipos de fracciones:

1. Fracciones homogéneas (1/4, 2/4, 9/4)
2. Fracciones heterogeneas (1/3, 2/5, 3/7)

Las fracciones homogéneas son las fracciones que tienen el mismo denominador; y las fracciones heterogeneas son las fracciones que tienen diferentes denominadores.

Resta de fracciones homogeneas

Las fracciones homogéneas, en resta, se restan los numeradores y el denominador se queda igual.

Ejemplos:
7/5 - 3/5 = 4/5
12/7 - 9/7 = 3/7

Resta de fracciones heterogéneas

Utilizando un algoritmo sencillo podemos aprender a restar fracciones mentalmente.

Veamos: Sean a /b y c/d dos fracciones cualesquiera. Si las deseamos restar podemos seguir la siguiente regla:

a/b - c/d = (ad - bc)/bd
se multiplica cruzado y los productos de restan / se multiplican los denominadores

Ejemplos:
2/3 - 1/2 = (2*2 - 3*1)/6 = (4-3)/6 = 1/6
5/3 - 7/8 = (5*8 - 3*7)/24 = (40 -21)/24 = 19/24
19 es un número primo, con lo cual no podemos simplificar más la fracción.

miércoles, 17 de febrero de 2016

ADICIÓN DE FRACCIONES HOMOGÉNEAS

ADICIÓN DE FRACCIONES HOMOGÉNEAS

Se llaman fracciones homogéneas a aquellas que comparten el mismo denominador por ejemplo (3/4 y 5/4) si no comparten el denominador las llamamos fracciones heterogéneas.

Si realizamos una suma o adición de fracciones homogéneas, debemos sumar los numeradores y mantener igual el denominador. Veamos un ejemplo de esto:

martes, 16 de febrero de 2016

EL PLANO CARTESIANO CON FRACCIONES

Pares Ordenados

(LAS CIUDADES MAS GRANDES DEL MUNDO) → es un PowerPoint informativo sobre las ciudades más pobladas del mundo y algunas condiciones de vida de estas.

♠ Par Ordenado

Es una pareja de elementos dados en cierto orden; estos elementos pueden ser numéricos o de otra clase. Los encontramos en la vida diaria de diferentes maneras, por ejemplo: el marcador de partidos deportivos entre dos equipos, los pares entre: pais-capital; provincia-capital; esposo-esposa; nombres-apellidos, nombre-edad, etc.

Nosotros estudiaremos los pares ordenados numéricos; con naturales, fracionarios y decimales.

♠ Concepto.-

(x, y) es un par ordenado cualquiera, x ≠ y, en donde x es el primer elemento llamado primera componentey y es el segundo elemento llamado segunda componente.

IMPORTANTE: (x, y) ≠ (y, x). Es decir el orden de las componentes no puede ser cambiado.

Estas componentes numéricas, se pueden graficar en los ejes cartesianos o plano cartesiano; la primera componente representa la abscisa y se ubica en el eje x; la segunda componente representa la ordenada y se ubica en el eje y. (x, y).

♠ Plano Cartesiano

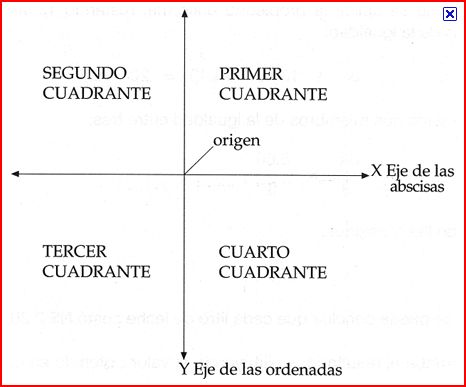
LLamado también Sistema Cartesiano de Coordenadas, está formado por dos rectas numéricas cortadasperpendicularmente; el punto de corte de estas rectas es el origen o cero y a partir de allí se ubican los números ordenadamente en las 4 direcciones (arriba, abajo, derecha e izquierda). A la recta horizontal se le llama eje x o de las abscisas; y la recta vertical se llama eje y o de las ordenadas.

En el eje x a la derecha están los números positivos.

En el eje x a la izquierda están los números negativos.

En el eje y arriba están los números positivos.

En el eje y abajo están los números negativos.

Ejemplos de nuestro gráfico:

R (-4, 4)

S (-1, 2)

U (-3, 0)

T (-2, -1)

V (3, 1)

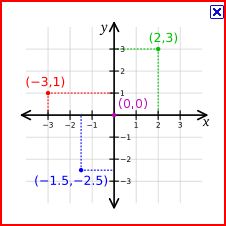
Para ubicar pares ordenados en el plano cartesiano, se le debe ubicar a la 1° componente en el eje x(horizontal), y la 2° componente en el eje y (vertical); dirigir segmentos paralelos (cuadricula) a los ejes hasta que se corten y allí se ubicará el punto que corresponde al par ordenado.

Las coordenadas o ejes cartesianos por ser dos rectas que se cortan en un punto forman cuatro cuadrantesque se cuentan o enumeran en forma antihoraria, comenzando por el de la derecha y superior, así:

lunes, 15 de febrero de 2016

CONCEPTO DEL PLANO CARTESIANO

Qué es el Plano cartesiano:

Como plano cartesiano se conoce como 2 rectas numéricas perpendiculares, una horizontal y otro vertical, que se cortan en un punto llamado origen o cero del sistema. Su nombre cartesiano se debe al filósofo y matemático francés René Descartes.

Un plano cartesiano está formado por4 cuadrantes o áreas producto de la unión de 2 rectas perpendiculares u coordenadas ortogonales y, 2 ejes conocidos como: el eje de las abscisas, ubicado de manera horizontal, identificado con la letra X y, el eje de las ordenadas, situado de manera vertical y, representado con la letra Y.

La finalidad del plano cartesianoes parejas de puntos llamadas coordenadas que se forman con un valor X y un valor Y representado como P(X,Y) por ejemplo: P(3,4) se puede observar que el 3 pertenece al eje de las abscisas y, el 4 al eje de las ordenadas.

Asimismo, sirve para analizar matemáticamente figuras geométricas como: parábola, hipérbole, línea, circunferencia y eclipse, los cuales forman parte de la geometría analítica.

Funciones en un plano cartesiano

Una función representada como: f(x)=y es una operación para obtener de un variable independiente (dominio) las variables dependientes (contra dominio). Por ejemplo: f(x)=3x

Función de x	Dominio	Contra dominio
f(2)=3x	2	6
f(3)=3x	3	9
f(4)=3x	4	12

La relación del dominio y el contra dominio es biunivoca significando que tiene solo dos puntos correctos.

Para encontrar la función en un plano cartesiano se debe primero tabular, o sea, ordenar los puntos en una tabla las parejas encontradas para posicionarlas o ubicarlas después en el plano cartesiano.

X	Y	Coordenada
2	3	(2,3)
-4	2	(-4,2)
6	-1	(6,-1)

También puede interesarte leer sobre el significado de "pienso, luego existo" de René Descartes.